Simulador Rompecabezas Torres de Hanoi

Hace un par de meses nos mandaron realizar una práctica bastante curiosa sobre las Torres de Hanoi en Algorítmica. Conocía el juego desde pequeño pero siempre me había parecido un coñazo jugarlo ya que, comparado con otros, es bastante aburrido. Resumidamente nos pedían modelar el juego mediante la especificación de estructuras de datos y funciones.
Analizar el recorrido que realizaba el algoritmo recursivo mas simple que se te puede ocurrir (el código se encuentra lineas mas abajo) sobre el árbol de soluciones (in-orden en este caso) y realizar una transformación de dicho algoritmo a una versión iterativa (mediante técnicas profesionales: inmersiones, plegados…). Tras realizar todos los puntos me quede con las ganas de ver si verdaderamente funcionaban bien los algoritmos por lo que desarrollé un pequeño simulador gráfico que resuelve el rompecabezas con el menor numero de movimientos posibles. Dicho esto voy a contar algo mas sobre este rompecabezas y su funcionamiento.
Según una leyenda india, en el Templo de Benarés, bajo el domo que marca el centro del mundo, hay una placa de latón con tres agujas de diamante. Durante la creación, Dios puso sesenta y cuatro discos de oro puro de distinto tamaño en una de las agujas, formando una torre. Los bramanes llevan generaciones cambiando de lugar, uno a uno, los discos de la torre entre las tres agujas de forma que en ningún momento un disco mayor descanse sobre otro mas pequeño. Cuando hayan conseguido trasladar todos los discos a otra aguja su trabajo estará terminado, y la torre y el templo se derrumbarán, y con un gran trueno, el mundo se desvanecerá.
Las torres de hanoi es un rompecabezas inventado en 1883 por el matemático Éduard Lucas. La leyenda citada arriba no fue mas que un invento publicitario del mismo creador con el que llamar la atención de la gente.
Consiste en un conjunto de 8 discos (en realidad puede variar desde 1 hasta n discos) de radio creciente que se apilan en una (la primera) de las tres torres del juego. El objetivo es conseguir trasladar toda la pila de discos de la torre inicial hacia una de las otras dos torres (generalmente a la ultima) teniendo en cuenta las siguientes restricciones:
- Solo se puede mover un disco cada vez.
- Un disco de mayor tamaño no puede colocarse sobre otro de menor tamaño.
- Solo puedes mover el disco que se encuentre en la cima de una de las torres.

Para saber el minimo numero de movimientos en el que se puede resolver el rompecabezas se sabe mediante:
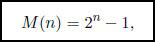
Con n = 8 (máximo número de discos que el simulador representa por temas de espacio en la pantalla) el mínimo numero de movimientos es de 255. Este numero crece de forma exponencial cuantos mas discos añadas, es por eso que la leyenda citada arriba (con n = 64) implicaría un numero de movimientos igual a 18.446.744.073.709.551.615 lo que haría que suponiendo que se moviera un disco por segundo, se tardarían quinientos ochenta mil millones de años en finalizar el rompecabezas.
El algoritmo recursivo que resuelve este problema es bastante simple de pensar e implementar. Aquí os dejo el código en java.
1 2 3 4 5 6 7 8 9 10 11 | private void hanoiRec(int n, Torre origen, Torre auxiliar, Torre destino){ //Caso directo if(n==1){ movimientos.add(new Movimiento(n, origen, auxiliar, destino)); }else{ //caso recursivo hanoiRec(n-1, origen, destino,auxiliar); movimientos.add(new Movimiento(n, origen, auxiliar, destino)); hanoiRec(n-1, auxiliar, origen, destino); } } |
La versión iterativa que implemente es algo mas compleja:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | private void hanoiIter(Movimiento arbol){ Stack<Movimiento> pila = new Stack<Movimiento>(); while (arbol.tieneHijoIzquierdo()){ pila.push(arbol); arbol = arbol.hijoIzquierdo(); } pila.push(arbol); while (!pila.isEmpty()){ arbol = pila.pop(); movimientos.add(arbol); while (arbol.tieneHijoDerecho()){ arbol = arbol.hijoDerecho(); while (arbol.tieneHijoIzquierdo()){ pila.push(arbol); arbol = arbol.hijoIzquierdo(); } pila.push(arbol); } } } |
Simulador
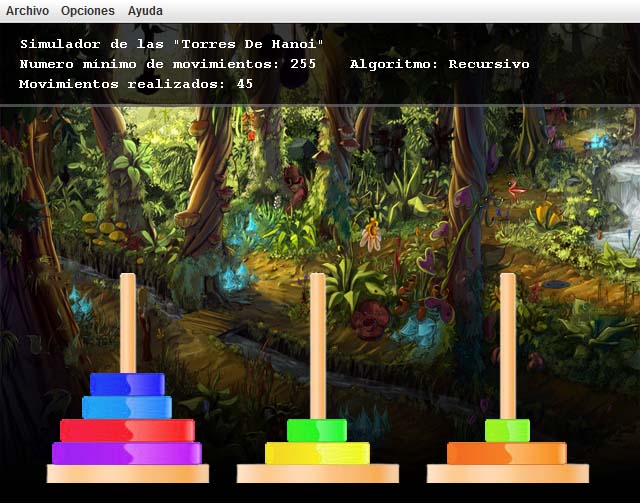
El simulador implementado permite utilizar uno de los dos algoritmos expuestos arriba para resolver el rompecabezas con un numero de discos que puede oscilar entre 1 y 8.
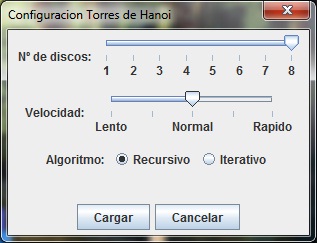
Para realizar las configuraciones (modificar numero de discos, velocidad en la que se realiza la animación y algoritmo usado) tendremos que ir a Opciones -> Configuración. Nos aparecerá un dialogo como el siguiente:
Podremos pausar y reiniciar el rompecabezas en cualquier momento de la animación a través del menú desplegable Archivo.
Podéis ver su funcionamiento en el siguiente vídeo.
Os dejo todo el proyecto y el ejecutable (el codigo esta liberado bajo una licencia GPL v3) para que podáis probar y mejorar el simulador. La contraseña para descomprimir es: truebaj.com
Cualquier cosa comentad en el post o en la seccion del juego en Proyectos.
11 Comentarios
Deja un comentario a truebaj
Categorías
- Blender (1)
- Desarrollo (8)
- Diseño web (1)
- General (4)
- Sin categoría (2)
Archivos
- septiembre 2014 (1)
- febrero 2014 (1)
- octubre 2013 (1)
- marzo 2013 (1)
- febrero 2013 (1)
- abril 2012 (1)
- marzo 2012 (9)





Muy bueno tu post, hace un tiempo escribí un post sobre las torres de hanoi en Puntopeek.com, pero los códigos son en C#, asi que te pongo un link para los q quieran descargar tu aplicacion. Saludos y suerte con el blog.
Gracias!C# o Java parecidos son en los dos lenguajes :). Espero que te sirva la aplicación y gracias por lo del link!
Ya esta Trueba salvándonos la vida con algorítmica. Está muy bien explicado!
Espero que te sirva Zoraida! Cualquier cosa me dices
Descargue tu archivo pero me pide un clave :S necesito el jeugo y modificarlo con las exigencias que me dice el profesor, si puedes decirme cual es la clave te lo agradeceria
^^ ya la vi
Hola que tal Trueba se me hizo interesante tu programa crees que puedas enseñarme hacerlo desde cero es que me lo dejaron pero no se hacerlo en grafico?
Gostei muito do projecto. nota 100
gostei muito projecto. nota 100, obrigado
hola buenas tardes me gusto mucho el trabajo que realizaste me podrias pasar me tal y como lo tienes el programa para ejecutarlo en java por favor te lo agradeceria de corazon
para poder ejecutarlo el proyecto netbeans por favor necesito ses favorsote